Math: What is the right Aspect Ratio?

In the shower the other day, I thought up an interesting question: what is the right aspect ratio to work in? (With, of course, the immediate follow-up question: what does "right" mean in this context?) In this post, I'll attempt to answer both questions with some simple math.

Setup

I've been doing some pre-production work on a storybook game for iOS devices. The game will likely be composed of full-screen scenes with hand-drawn background plates. I don't want to have require new background plates for every resolution (much less aspect ratio), so the plan is to create one background and fit it to the screen.

So, depending on the screen aspect ratio (in this case: 4:3 on the left, 16:9 on the right), some of the image will be cropped, either off the sides or off the top and bottom.

Minimizing Waste

Since I'm not of a mind to have something drawn that isn't needed, one possible definition of "right" aspect ratio is the one that minimizes wasted area in the background image. So how much area is wasted?

Well, denoting the aspect ratio of the screen s and the aspect ratio of the background image b, and -- without loss of generality -- assuming the screen height is 1, it is easy to draw a picture of the situation:

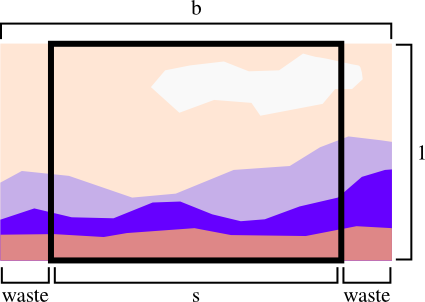
So, if the background is wider than the screen, the percentage of the background image wasted is (b-s) / b. Similarly, when the background is narrower, the waste is (1/b-s) / (1/b).

As expected, on a 4:3 screen a background image of aspect ratio 4:3 wastes the least.

Of course, on iOS one needs to worry about three aspect ratios: 4:3 [iPad], 3:2 [iPhone <= 4], and 71:40 [iPhone >= 5]. (In case you are wondering, 71:40 is 'nearly 16:9'.):

NOTE: I'm only considering landscape aspect ratios because that's the target for this game.

Assuming one wants to give equal weight to background waste on each device, the proper aspect ratio of the background image should minimize the sum of these three curves.

This minimization happens at the 3:2 aspect ratio. Indeed, my intuition is that with equally-weighted devices the minimum-waste aspect ratio will always be the median aspect ratio.

Maximizing Excitement

In the previous section, I counted areas of the background for each time they were cropped -- that is, background that didn't show at 4:3 and at 3:2 was counted as being twice as bad as background that was only cropped at 3:2. Perhaps, instead of obsessing over these lost pixels, one should instead maximize the percentage of the background that is cropped by no device (i.e. the part of the background every screen sees).

What is this percentage? Consider a background of size bx1 to be shown on screens of aspect s1, ..., sN. The width of the visible-on-all-screens region is w = min(b, s1, ..., sN), because the background will be cropped after its aspect exceeds the smallest screen aspect. The height of the visible region is h = min(1, b / s1, ..., b / sN), because of cropping on the top and bottom of edge of the background when it is scaled to the widest aspect ratio. (More intuition: consider scaling the visible region to [horizontally] fit a screen of size sx1. The scale factor is s / b, so it must be the case that h * s / b <= 1; thus h <= b / s.)

Putting these figures together gives percentage 100 * min(b, s1, ..., sN) * min(1, b / s1, ..., b / sN) / (b * 1). Interestingly, this means that maximizing visible area only depends on the narrowest and widest aspect ratio under consideration:

The unfortunate news is that with aspect ratios of 4:3 and 71:40 in the mix there isn't any background size that doesn't end up with about 25% of its area not visible on all screens. The fortunate news is that the best aspect ratio in terms of waste (3:2) is within this 75%-used plateau.

Going Further

In this article I didn't talk at all about foreground content (which must be scaled to fit within each aspect ratio), and only explored two objective functions. Other interesting objective functions might include one weighted for all browser sizes, or one that is concerned with fairness (forcing all screens to lose about the same area of the background).

If you have other ideas, feel free to leave a comment or send an e-mail.